Min/Maxing Newcomb's Paradox

And the Foibles of Philosophers as Puzzle Gamers

Much indeed has been written about Newcomb’s Paradox, but like with a number of other perennial debates, there appears to be no stomping out the fire, even though there’s a right answer (of which I hope to convince you shortly).

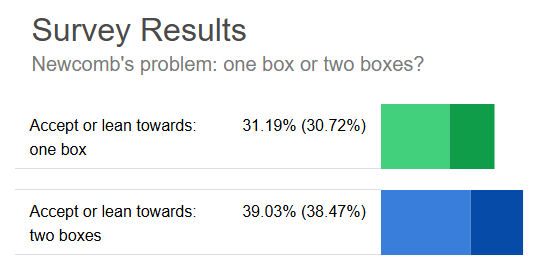
Look at this PhilPapers Survey:

How could this be? Situations like this are both baffling yet instructive; they can clue us in to features of thought experiments that really hang people up, even very smart & sincere people. Once we recognize those features, we can better notice them when they show up in other places.

And this is really good, because we don’t want to fall into the trap of thinking that big groups of smart & sincere people are just completely unreliable. We like big groups of smart & sincere people, generally! And so if we can explain when and why they become unreliable, then it’s not so bad; we can adjust our level of reliance contextually, like how you can trust your friend Bill to help you move something at the drop of a hat — just never on weekends.

(Or, if you’re sinister, you can use these findings to mess with people using increasingly elaborate thought experiments, giving yourself all sorts of attention and clicks and things.)

To begin, we’ll set the stage by discussing certain hiccups that affect even very smart & sincere people. After that, we’ll talk about how these take shape in Newcomb’s Paradox.

The Overpower Principle Rocks!

In game theory, there are a number of principles that we can elect to use or ignore. One of them is the “Overpower Principle.” The Overpower Principle says that it is most rational to make the decision that involves opening the most things and taking what’s inside.

Now, you may not have heard about this principle before.

That’s okay. I made it up. You just need to know that it rocks!

In game theory you often find boxes (or doors, or whatever) with different amounts of money in them. The Overpower Principle says, “Hey, open the most you can! It’ll probably get you the most money, right?” And that’s great, because you want money, the more the better.

Let’s say you’re playing a game where there are 3 boxes through door A, and 2 boxes through door B. You don’t know how much money is in the boxes, and once you pick a door and go through, it closes and locks.

“No problem,” says the Overpower Principle. “Choosing door A is rational. There are 3 boxes there. 3 is more than 2. Door A overpowers door B.”

But before you can act, you learn another detail of the scenario. You are informed that the 3 boxes behind door A contain no money, and that the 2 boxes behind door B contain $100 apiece.

Now things are different, right? You just learned materially relevant information, spoiling the contents of the boxes and making the correct choice, door B, completely obvious — you would think.

The problem is that choosing door 2 is irrational. Yes, it might get you more money. But it’s not rational to do that, per the Overpower Principle. You see, the Overpower Principle is determining what “rational” means. Furthermore, the Overpower Principle does not, and cannot, know this new information you just got.

That may be an important consideration for you, a person who wants money, but it’s of no consideration for the Overpower Principle, and that’s the criterion for ‘rationality’ here.

Then again, perhaps…

The Overpower Principle Sucks

Door A may overpower door B, but that doesn’t mean it’s the correct move if we want money in this situation given what we have learned. But, look what’s going on: The principle’s formidable name, how it is described when its dictated choice stomps & thwomps the alternative, and its claim to determining “rationality.” This principle already has a head start in the battle for hearts & minds. If we want to defend the alternative choice, we’re put on the back foot; we’re defending the underpowered choice. We’re enemies of rationality itself.

Even smart & sincere people fall for this. It’s a common foible, and when someone is tripped up by such a foible, we can say they’ve been Foibled accordingly. That is, if they are uncritical about the conditions by which some principle may betray them, and uncritical about how “rationality” is being defined, there’s a danger that they get swept away by such a principle, under such conditions. It won’t happen to all smart & sincere people, but it may stumble some share of them.

Hence we have our first Foible:

• Foible #1: “Sometimes even smart & sincere people are swept up by what a principle is called and its way of dictating if a choice is ‘rational’… even if following the principle clearly fails to pay off under some conditions.”

Let’s keep going!

The next concerns when “possibility” has different meanings.

How Could Both Be Possible!?

Take a coin, put it in a cup, shake it around, and then slam it (upside down) on a table. Listen to the coin fall, but keep its result hidden under the cup.

In this situation, the result is possibly heads and possibly tails.

You might feel some discomfort as I said that. After all, the coin is already fallen. It can’t be both. It’s only “however-it-fell” and it’s not possibly “the-other-way.” You can easily imagine a privileged observer — perhaps the table is made of glass (err… careful with the slamming, there!) and your friend Bill is underneath — who can see exactly what the result in fact is. So, it’s not possibly heads or tails; it’s only the face that Bill doesn’t see from below.

“Possibility” is whatever isn’t ruled out. But ruled out per what? It turns out that the term has a zillion different meanings, because there are a zillion different sources to index the term against.

(To be clear: The phrase “possibly X” has no meaning except per that to which the “possibly” is indexed. It means “X isn’t ruled out by ___.” See that blank? That’s really bad, but people just keep on using “possibly X” anyway, unindexed, vacuous, sloppy, dangerous. Stay vigilant.)

Here, since the cup blocks my view, I can’t rule out heads, and I can’t rule out tails. Therefore, for me, heads is possible (not ruled out by what I see) and tails is possible (also not ruled out by what I see).

But for Bill, the result is heads, so heads is possible (not ruled out by what Bill sees), and tails is not possible (because it’s ruled out by what Bill sees).

Now, if you were put into a game theoretic situation where this coin result is involved, how should you think of it, prior to the cup being lifted? For the purposes of the game, you should treat it as if it hadn’t been decided yet. You should imagine it like “Schrödinger’s Coin,” unmaterialized, undetermined. It doesn’t matter that the coin was flipped a few seconds ago, a few days ago, or a few years ago. For the purposes of the game, lifting the cup decides the coin.

Weird, I know. Counterintuitive. But, intuitions are often prone to Foibling.

• Foible #2: “‘Possibility’ is polysemous; it has many different meanings, and when a game situation mixes scopes, things can become very counterintuitive, even for very smart & sincere people.”

And now we come to our Final Foible.

Omniscient Storytelling & (Too-)Active Listening

Much fiction features an “omniscient narrator” that somehow knows all sorts of juicy details that may not be plausibly accessible in any real-world situation. As long as it sounds vaguely conceivable, we give our storyteller the benefit of the doubt and let him mold our framings. A storyteller might give us infallible knowledge about fake barns along a country highway. A storyteller may promise us that Mary “had all the physical information” prior to leaving the room. A storyteller may swear that an entity can behave just like one with consciousness without itself having consciousness at all.

Sometimes we raise an eyebrow and reject their stories as smuggling dubious assumptions. Sometimes we acknowledge those assumptions, but critique the degree to which we can be confident about the relationship between those assumptions and the conclusions drawn. Sometimes we acknowledge those assumptions, but we’re worried that the story is disanalogous to more realistic contexts in ways that undermine conclusions drawn for those contexts.

But often enough, we don’t do any of those things — rather, we give the implausibly enlightened storyteller the benefit of the doubt, let him sweep us downriver to a bespoke conclusion, and then mistakenly think something very interesting & important has been revealed about the real world and/or the cherished concepts we use to make sense of it.

Even worse, sometimes we go with the storyteller partway, but make small corrections in our minds to account for the details we don’t accept. So those who would otherwise reject the premise continue to “play,” but from a strange middle place of subsurface ambiguity, a major source of self-sustaining chatter.

And, of course, sometimes the storyteller sets things up in a way where such confusion is inevitable (e.g., where some will naturally interpret things one way, and others another way).

• Foible #3: “In thought experiments, omniscient narrators take many licenses, and how we respond to those licenses vary. Our relationship to storytellers and their stories is one of interactivity and even mutation; iffy assumptions can be ignored, embraced, altered, or obscured in service to ‘staying involved in the discussion’ as a social pattern. This yields a selection effect where people who boldly reject the story become discursive ‘non-players’; the rest are Story-Accepters and Half-Committers, often talking (and talking and talking) past one another. And for some stories, even the Story-Accepters may have different ideas of how to interpret the story.”

Foible Fest

What happens if you start with a bunch of smart & sincere people, but then you subject them to a thought experiment and trailing discourse where the above 3 Foibles are at play?

Newcomb’s Paradox is a Foible Fest. It is a thought experiment constructed in good faith but has each of the above Foibling features, spawning a polarizing chatter party for any who choose to engage as “players” of the discourse’s puzzle game.

Let’s review Newcomb’s Paradox real quick:

Suppose a being in whose power to predict your choices you have enormous confidence. (One might tell a science-fiction story about a being from another planet, with an advanced technology and science, who you know to be friendly, etc.) You know that this being has often correctly predicted your choices in the past (and has never, so far as you know, made an incorrect prediction about your choices), and furthermore you know that this being has often correctly predicted the choices of other people, many of whom are similar to you, in the particular situation to be described below. One might tell a longer story, but all this leads you to believe that almost certainly this being's prediction about your choice in the situation to be discussed will be correct. There are two boxes, (Bl) and (B2). (Bl) contains $1000. (B2) contains either $1,000,000 ($M), or nothing. What the content of (B2) depends upon will be described in a moment.

You have a choice between two actions:

(1) taking what is in both boxes

(2) taking only what is in the second box.

Furthermore, and you know this, the being knows that you know this, and so on:

(I) If the being predicts you will take what is in both boxes, he does not put the $M in the second box.

(II) If the being predicts you will take only what is in the second box, he does put the $M in the second box.

The situation is as follows. First the being makes its prediction. Then it puts the $ M in the second box, or does not, depending upon what it has predicted. Then you make your choice. What do you do?

And now let’s backtrack through our Foibles and see how Newcomb’s Paradox features them.

Re: Foible #3. To describe an entity as a perfect predictor takes licenses about whether a person’s decisions are perfectly predictable, which might invite complaints from some folks. But, “just nearly perfect — enormous confidence of success” to placate such folks only makes things worse: It seems to address those who would find a perfect predictor implausible, but takes the very same licenses. Either we know nothing about the final predictive success rate, or we know something (e.g., it’s 100%, or 99%, or 60%, etc.).

If the former, there is no paradox; there’s rumors about some dude being a good guesser that you can take or leave.

If the latter, you can boringly plug that value into your reward math:

• Reward(1box) = $1,000,000 * P(correct prediction)

• Reward(2box) = $1,000 + ($1,000,000 * (1 - P(correct prediction)))

Re: Foible #2. The reader imagines themselves in the situation with the value already “locked-in,” a bit like the coin-under-cup.

Now, if we were in a perfect prediction situation, it’s easy to see the strange “time travel” effect at play: Whatever choice you make determines the content of the second box retroactively (well, not quite… let’s say retromodally). Here it’s more obvious that the content of the box should not be seen as “locked-in” at all; it should be seen as our Schrödinger’s Coin from earlier, with the content in flux as indexed to what you can see (possibly empty, possibly full), and weighted according to the predictor’s aptitude, plus whichever of the two choices you make.

But when we downgrade our predictor to merely “pretty good at predicting,” many of us feel ourselves ejecting out of that sci-fi-feeling place, and we retreat back to more mundane feelings about “locked-in” box content. This leaves us susceptible to…

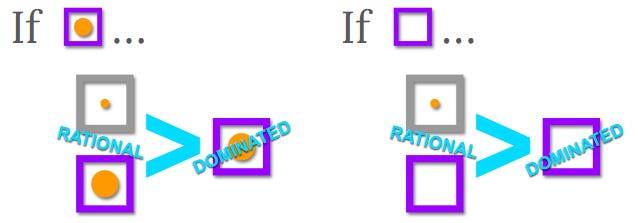
Re: Foible #1. … the “Dominance Principle.”

The Dominance Principle says that it’s rational, among 2 or more options, to pick the option that is always at least as good or better than the others, if there is such an option.

When you have “locked-in” content — where the decision you make has zero retromodal relationship whatsoever to the predictor’s call and, in turn, what the box contains — the Dominance Principle says to take both boxes. After all, if the box is full, taking both boxes gets you $1000 more than if you take one box; if the box is empty, taking both boxes also gets you $1000 more than if you take one.

But this framing provides a locked-in antecedent, then asks you what to do from there. It totally disregards the fact that the choice you make has a bizarre retromodal “tether” back to the predictor.

And we were primed to disregard this because of the earlier Foibles:

• First, we either chalk the predictor as perfect predictor (making the answer trivial, ending the discursive game), or we reject the predictor entirely (quitting the discursive game), or we accept the predictor as “very probably right, but maybe not,” simultaneously floating “he’s quite good at prediction!” while refusing to commit to a success rate, leaving us in a meaningless murk and susceptible to the rest.

• Then, for those of us still playing the game, we’ve lost sight of that on which the box contents depends: The prediction, which in turn depends on whatever is chosen. Rather, in this new murky world, the prediction feels irrelevant; the choice made has zero ramification upon the box contents.

Slowly but surely, we (who stay discursive players) are escorted into a situation where we’re entirely ignoring the predictor and the retromodal oddity he represents, only pretending to be playing along with a predictor scenario (enabled by the mealy-mouthed premise that threw predictive success into the murk).

Then, having disregarded it, the “Dominance Principle” stomps over and makes its pelvic gyrations toward taking 2 boxes. With those crucial considerations out of mind, we’re subject to its definition of rationality, just like the “Overpower Principle” told us it was “rational” to open more boxes even when we knew the contents were worse.

But… there’s hope.

Defoibling with “NewcoMax”

All we have to do is create an alternative scenario that specifically targets where things went Foibly. Then any smart & sensible person can follow along to the boring, plain conclusion of “1 box.”

First, let’s build a perfect predictor that everyone can agree on.

Instead of predicting a human choice, we’ll say that the predictor, named Engineer, predicts the behavior of a complex software program called NewcoMax, and loading (or not) the opaque box according to the option that Engineer predicts NewcoMax will select this time. Once it begins, NewcoMax takes 10 minutes to make a choice between “1 box” or “2 box,” but Engineer knows well in advance what NewcoMax will select because Engineer is totally familiar with NewcoMax’s complicated functionality.

Oh, one more thing: You get the money that NewcoMax earns.

Now, 5 minutes into this process, you and I don’t know the content of the second box. It’s possibly empty, possibly full from our vantage point.

And now I ask you: Which of “1-boxer” or “2-boxer” do you hope NewcoMax is?

And of course you respond, loudly, with confidence & correctness greater than hundreds of very bright surveyed philosophers: “I hope it’s a 1-boxer!”

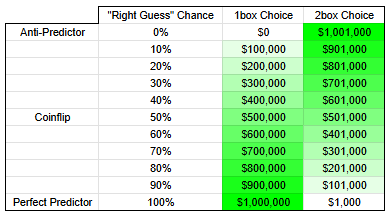
From here, we can reduce the probability of Engineer’s predictive success (perhaps the program’s functionality is so complicated that Engineer can only make very good predictions, but not perfect ones), and we get something like our lovely Excel chart from earlier, where you likewise shout “1-boxer!” as long as Engineer is somewhat better than a coinflip.

Notice what we just accomplished: By externalizing the choicemaker and turning him into something more mundane, all of this Dominance Principle stuff, worries about retrocausality, rabbit trails about free will, etc. don’t even enter our minds. The right answer is as lucid as can be.

“But that isn’t Newcomb’s Paradox,” Bill says, bonking his head on the glass table as he struggles to get out from under it. Groaning, he stands up and mutters, “Your version is disanalogous in… ouch… material ways…”

But of course it is different. It has been Defoibled!

The point is this: You can take any boring dilemma and Enfoible it to spawn a self-advertising puzzle that drives its own virulence & engagement.

First (Foible #3), you can make your scenario implausible. People react to implausible scenarios in diverse ways, sometimes very subtly; this “splays” interpretations, yielding confusion & chatter.

Second (Foible #2), you can use unindexed language, like possible (per what?), necessary (per what?), obligatory (per what?), supererogatory (per what?), value (per what?), epistemically justified (per what?), and rational (per what?), or (as in this case) build your scenario such that the reactive discourse will be full of these things. Each of those parenthetical danglers is a wide open question that folks are in the habit of pretending is closed, “splaying” interpretations, yielding confusion & chatter.

Third (Foible #1), you can pit the right answer against powerful general principles with “edge cases” that only seem to come up in contrived thought experiments. This sets “reason against reason” and drives people zany:

• Set “Don’t push large men off bridges to stop trolleys, it probably won’t work” against “No but in this scenario you know it will work, it will save 5 lives in fact” to make people question our normal moral expectations & reasoning.

• Set “Ella knows the eggs she bought at the store are in the fridge; she opens it and confirms” against “No but in this scenario Bill, without Ella’s knowledge, replaced those eggs with duplicate eggs” to make people question our everyday epistemic experience & framings.

• And so forth.

By “drives people zany,” I mean this “splays” people’s reactions according to which of the horns their various hunches latch onto as “obvious” (because it has to be one or the other, right?), yielding confusion & chatter.

Notice a pattern!?

I haven’t yet bothered to look, but wouldn’t it be funny if every thought-experiment-related PhilPapers Survey “toss-up” had such identifiable Foibling Features? It’s possible (that is, ‘not ruled out,’ per my ‘not yet bothering to look’)!

Anyway, some stuff to watch out for, fellow 1-boxer.

Or, uh, exploit.